Learnin’ LaTeX: Top Five Mind-Blowing Mathematical Equations in LaTeX
As extracurriculars wind down and lunch breaks are no longer super-saturated with meets and studying, it is now officially time to master the cryptic script of all mathematics and scientists: LaTeX. LaTeX is a type of markdown commonly used by millions of people worldwide in research papers and other scientific documents to easily format mathematical equations and other symbols.
The Challenge
In this challenge, I decided to learn LaTeX and write the top five mind-blowing mathematical equations, as determined by Sean Li. I started getting familiar with the syntax during the first lunch break, messing with lists and tables from Princeton’s Beginner’s Guide to LaTeX. On the second lunch break, I was joined by senior Yousuf Shafiu and junior Anneliese Coleman to finish the list (and teach them the little I knew of LaTeX as well). In all, we had less than two hours to learn and teach LaTeX and write five (later adjusted to six) mind-blowing mathematical equations (plus formulate the challenge). When working on the challenge itself, we started with writing the LaTeX on the whiteboard then used the Discord bot TeXit to quickly and collaboratively compile the code.
LaTeX — The Basics
The basic syntax of LaTeX was fairly straightforward, and I condensed them into five rules:
- To end “math mode” (where your text will be interpreted as math equations), surround the desired text with a single $ on both sides.
- To use special symbols in LaTeX, precede it with a \. (Want a symbol but don’t know what it is? Look it up!)
- Use _ to create a subscript and ^ to create a superscript. (This can also be used in summations and integrals.)
- Wherever you want to add parenthesis, use {} (curly brackets) instead (for quantities and groupings—everything but when you want the literal parenthesis symbol).
- To open and close some non-mathematical aspect of LaTeX, use \begin {insert_thing_here} and \end {insert_thing_here}.
Exploration
During the first lunch period, before jumping into the challenge, I explored LaTeX features using the guide and learned about the non-mathematical operations for LaTeX. First, I learned the basics of creating and compiling a document. Essentially, I could create sections using \section {Section Header}, begin and end documents with \begin {document} and \end {document}, import packages using \usepackage {insert_package_name_here}, create line breaks using \, add comments with %, and more. Next, I focused on learning three elements: ordered and unordered lists and tables.
Ordered lists begin and end with \begin {enumerate} and \end {enumerate} with the \item between. Unordered lists have the same syntax with {itemize} instead of {enumerate}.
\section{Ordered List}\begin {enumerate}
\item Euler’s Identity
\item Euler Product Formula
\item Gaussian Integral
\item Cardinality of the Continuum
\item Analytic Continuation of the Factorial
\end {enumerate}
\section{Unordered List}
\begin {itemize}
\item Euler’s Identity
\item Euler Product Formula
\item Gaussian Integral
\item Cardinality of the Continuum
\item Analytic Continuation of the Factorial
\end {itemize}
Creating tables is slightly more complicated. To create one, begin {tabular}, separate each column with &, and separate each row with \\.
\begin{tabular}{r|cl}
Number & Name \\
\hline
1 & Euler’s Identity \\
2 & Euler Product Formula \\
3 & Gaussian Integral \\
4 & Cardinality of the Continuum \\
5 & Analytic Continuation of the Factorial \\
\end{tabular}
For the challenge, I decided to use a table. After learning the basics of creating LaTeX structures, I felt ready to write equations, the main feature LaTeX prides itself on.
The Journey
The first equation I wrote was the trusty Euler’s identity. It was a fairly simple equation to start with. With this, I learned how to properly write exponents, $e^{x}$ and learned that π is denoted with $\pi$.
Next, I worked on the Euler product formula. This was trickier to master since it both had a summation and a product symbol. The format of the summation was straightforward enough, $\sum_{N}$. Next, the fraction was also fairly straightforward: $\frac {1}{N^s}$. The tricky part ended up being the product sign. Essentially, it was just uppercase pi, but in LaTeX, that was represented by $\prod$ to add the proper notation.
That wrapped up my lunch period alone. The next day, I had Yousuf with me, and after a quick briefing, we tackled the rest of the equations. When writing the Gaussian integral, we learned how to write integrals $\int$, infinity $\infty$, and square roots $\sqrt{\pi}$.
Next, the Cardinality of Continuum equation was a bit tricky with the real and natural number symbols. We ended up having to use $\mathbb{R}$ and $\mathbb{N}$ respectively to create the two symbols. Finally, the ~ symbol is denoted with $\sim$.
The fifth equation was straightforward enough, with no new symbols, so we quickly wrote and compiled the code.
At this point, we reached our goal of writing the top five equations from the list. So we began looking for other cool equations to write out. While we were trying to find the coolest form of the Schroeder equation, the amazing Anneliese visited, so we helped her learn LaTeX to write an equation of her choosing. She selected the explicit formula for the Fibonacci sequence. It took us a while to find how to write an uppercase phi, which ended up being $\varphi$. Once we figured it out, Anneliese wrote her equation.
And with that, we futilely searched for more fun equations then hurried over to class, satisfied with our LaTeX journey.
Final Product
Our final code, as shown in Overleaf, was:
\documentclass{article}
\usepackage{amsfonts}
\title{Learnin’ $\LaTeX$}
\author{Shreya Chaudhary, Yousuf Shafiu, Anneliese Coleman}
\date{March 2022}
\begin{document}
\maketitle
\section{Epic Mathematical Equations}
\begin{tabular}{r|cl}
Math Equation Name & Equation\\
\hline
Euler’s Identity & $ e^{i\pi} + 1 = 0 $ \\
Euler Product Formula & $\sum_{n} \frac {1} {n^s} = \prod_{p} \frac {1} {1 – \frac {1} {p^s}} $\\
Gaussian Integral & $\int_{-\infty}^\infty e^{-x^2} \mathrm dx = \sqrt{\pi}$\\
Cardinality of the Continuum&$\mathbb{R} \sim 2^{\mathbb{N}}$\\
Analytic Continuation of the Factorial&$n! = \int_0^\infty x^n e^{-x} \mathrm dx$\\
Explicit Formula for the Fibonacci Sequence & $F(n) = \frac{\varphi^n – (-\frac{1}{\varphi})^n}{\sqrt{5}}$\\
\end{tabular}
\end{document}
Odds and Ends
As we were dealing with a lot of cool equations, we could not resist exploring and appreciating the glorious mathematics before us. Here are a few cool things we found.
First, the Gaussian integral was epic. We graphed it using Desmos to see how the area under the curve could be $\sqrt{\pi}$ (√π).
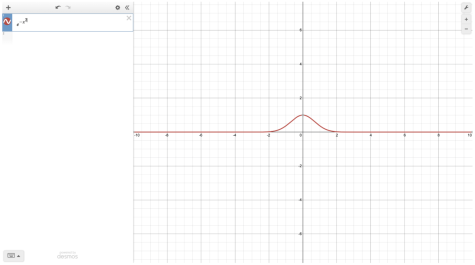
Seeing the graph makes the integral make more sense, but it’s regardless very, very cool.
Next, when we were trying to figure out the sign for natural numbers ($\mathbb{N}$), we ended up trying $\natural$ and we got… a musical natural! That was absolutely mind-blowing to us.
Conclusion
Overall, I had an absolute blast finally learning $\LaTeX$ with Yousuf and Anneliese. It was awesome to explore some basic features of the language and start getting familiar with it, and I can’t wait to explore it in more depth. Huge thanks to Yousuf and Anneliese for exploring the language with me and to Matthew Stagg for helping us out every now and then.
If you are interested in learning about $\LaTeX$ (and going deeper than this article), a few resources I would recommend are The Not So Short Introduction to LaTeX to learn and TeXnique to practice.
I can’t wait to continue exploring this popular markdown language!
Shreya Chaudhary is a senior planning to major in data science or computer science. She interns with TigerGraph, promotes and tutors women in STEM through...